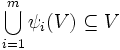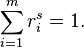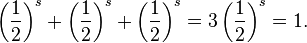|
| Estimating the Hausdorff dimension of the coast of Great Britain |
In
mathematics, the
Hausdorff dimension (also known as the
Hausdorff–Besicovitch dimension) is an
extended non-negative
real number associated with any
metric space. The Hausdorff dimension generalizes the notion of the dimension of a real
vector space. That is, the Hausdorff dimension of an
n-dimensional vector space equals
n. This means, for example the Hausdorff dimension of a point is zero, the Hausdorff dimension of a line is one, and the Hausdorff dimension of the plane is two. There are however many
irregular sets that have noninteger Hausdorff dimension. The concept was introduced in 1918 by the
mathematicianFelix Hausdorff. Many of the technical developments used to compute the Hausdorff dimension for highly irregular sets were obtained by
Abram Samoilovitch Besicovitch.

Sierpinski triangle. A space with fractal dimension log 3 / log 2, which is approximately 1.585
[edit]Informal discussion
Intuitively, the dimension of a set (for example, a
subset of
Euclidean space) is the number of independent parameters needed to describe a point in the set. One mathematical concept which closely models this idea is that of
topological dimension of a set. For example a point in the plane is described by two independent parameters (the
Cartesian coordinates of the point), so in this sense, the plane is two-dimensional. As one would expect, the topological dimension is always a
natural number.
However, topological dimension behaves in quite unexpected ways on certain highly irregular sets such as
fractals. For example, the
Cantor set has topological dimension zero, but in some sense it behaves as a higher dimensional space. Hausdorff dimension gives another way to define dimension, which takes the metric into account.
To define the Hausdorff dimension for a metric space
X as a non-negative
real number (that is, a number in the half-closed infinite interval [0, ∞)), we first consider the number N(
r) of
balls of radius at most
r required to cover
X completely. Clearly, as
r gets smaller N(
r) gets larger. Very roughly, if N(
r) grows in the same way as 1/
rd as
r is squeezed down towards zero, then we say
X has dimension
d. In fact the rigorous definition of Hausdorff dimension is somewhat roundabout, as it allows the covering of
X by balls of different sizes.
For many shapes that are often considered in mathematics, physics and other disciplines, the Hausdorff dimension is an integer. However, sets with non-integer Hausdorff dimension are important and prevalent.
Benoît Mandelbrot, a popularizer of
fractals, advocated that most shapes found in nature are fractals with non-integer dimension, explaining that
"clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line." [1]There are various closely related notions of possibly fractional dimension. For example
box-counting dimension, generalizes the idea of counting the squares of
graph paper in which a point of
X can be found, as the size of the squares is made smaller and smaller. (The box-counting dimension is also called the
Minkowski-Bouligand dimension). The
packing dimension is yet another notion of dimension admitting fractional values. These notions (packing dimension, Hausdorff dimension, Minkowski-Bouligand dimension) all give the same value for many shapes, but there are well documented exceptions.
]Formal definition
Let
X be a
metric space. If

and

, the
d-dimensional
Hausdorff content of
S is defined by

In other words,

is the
infimum of the set of numbers

such that there is some (indexed) collection of
balls 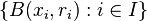
covering
S with
ri > 0 for each
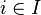
which satisfies

. (One can assume, with no loss of generality, that the index set
I is the natural numbers
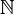
. Here, we use the standard convention that
inf Ø =∞.) The
Hausdorff dimension of
X is defined by

Equivalently,

may be defined as the
infimum of the set of

such that the
d-dimensional
Hausdorff measure of
X is zero. This is the same as the supremum of the set of

such that the
d-dimensional Hausdorff measure of
X is infinite (except that when this latter set of numbers
d is empty the Hausdorff dimension is zero).
[]Examples
- The Euclidean space Rn has Hausdorff dimension n.
- The circle S1 has Hausdorff dimension 1.
- Countable sets have Hausdorff dimension 0.
- Fractals often are spaces whose Hausdorff dimension strictly exceeds the topological dimension. For example, the Cantor set (a zero-dimensional topological space) is a union of two copies of itself, each copy shrunk by a factor 1/3; this fact can be used to prove that its Hausdorff dimension is ln2 / ln3, which is approximately 0.63 The Sierpinski triangle is a union of three copies of itself, each copy shrunk by a factor of 1/2; this yields a Hausdorff dimension of ln3 / ln2, which is approximately 1.58.
- Space-filling curves like the Peano and the Sierpiński curve have the same Hausdorff dimension as the space they fill.
- The trajectory of Brownian motion in dimension 2 and above has Hausdorff dimension 2 almost surely.
- An early paper by Benoit Mandelbrot entitled How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension and subsequent work by other authors have claimed that the Hausdorff dimension of many coastlines can be estimated. Their results have varied from 1.02 for the coastline of South Africa to 1.25 for the west coast of Great Britain. However, 'fractal dimensions' of coastlines and many other natural phenomena are largely heuristic and cannot be regarded rigorously as a Hausdorff dimension. It is based on scaling properties of coastlines at a large range of scales, but which does not however include all arbitrarily small scales, where measurements would depend on atomic and sub-atomic structures, and are not well defined.
- The bond system of an amorphous solid changes its Hausdorff dimension from Euclidian 3 below glass transition temperature Tg (where the amorphous material is solid), to fractal 2.55±0.05 above Tg, where the amorphous material is liquid.[2]
[]Properties of Hausdorff dimension
[]Hausdorff dimension and inductive dimension
Theorem. Suppose X is non-empty. Then

Moreover

where
Y ranges over metric spaces
homeomorphic to
X. In other words,
X and
Y have the same underlying set of points and the metric
dY of
Y is topologically equivalent to
dX.
These results were originally established by
Edward Szpilrajn (1907–1976). The treatment in Chapter VII of the Hurewicz and Wallman reference is particularly recommended.
[]Hausdorff dimension and Minkowski dimension
The
Minkowski dimension is similar to the Hausdorff dimension, except that it is not associated with a measure. The Minkowski dimension of a set is at least as large as the Hausdorff dimension. In many situations, they are equal. However, the set of
rational points in
[0,1] has Hausdorff dimension zero and Minkowski dimension one. There are also compact sets for which the Minkowski dimension is strictly larger than the Hausdorff dimension.
[]Hausdorff dimensions and Frostman measures
If there is a
measure μ defined on
Borel subsets of a metric space
X such that
μ(X) > 0 and

holds for some constant
s > 0 and for every ball
B(x,r) in
X, then

. A partial converse is provided by
Frostman's lemma.
That article also discusses another useful characterization of the Hausdorff dimension.
[]Behaviour under unions and products
If

is a finite or countable union, then

This can be verified directly from the definition.
If
X and
Y are metric spaces, then the Hausdorff dimension of their product satisfies
[3]
This inequality can be strict. It is possible to find two sets of dimension 0 whose product has dimension 1.
[4] In the opposite direction, it is known that when
X and
Y are Borel subsets of

, the Hausdorff dimension of

is bounded from above by the Hausdorff dimension of
X plus the
upper packing dimension of
Y. These facts are discussed in Mattila (1995).
[]Self-similar sets
Many sets defined by a self-similarity condition have dimensions which can be determined explicitly. Roughly, a set E is self-similar if it is the fixed point of a set-valued transformation ψ, that is ψ(E) = E, although the exact definition is given below.
Theorem. Suppose

are
contractive mappings on
Rn with contraction constant
rj < 1. Then there is a unique
non-empty compact set
A such that

To determine the dimension of the self-similar set A (in certain cases), we need a technical condition called the open set condition on the sequence of contractions ψi which is stated as follows: There is a relatively compact open set V such that
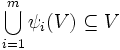
where the sets in union on the left are pairwise
disjoint.
Theorem. Suppose the open set condition holds and each ψ
i is a similitude, that is a composition of an
isometry and a
dilation around some point. Then the unique fixed point of ψ is a set whose Hausdorff dimension is
s where
s is the unique solution of
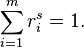
Note that the contraction coefficient of a similitude is the magnitude of the dilation.
We can use this theorem to compute the Hausdorff dimension of the Sierpinski triangle (or sometimes called Sierpinski gasket). Consider three
non-collinear points a1,
a2,
a3 in the plane
R² and let ψ
i be the dilation of ratio 1/2 around
ai. The unique non-empty fixed point of the corresponding mapping ψ is a Sierpinski gasket and the dimension
s is the unique solution of
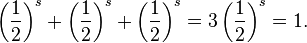
Taking natural logarithms of both sides of the above equation, we can solve for s, that is:

The Sierpinski gasket is self-similar. In general a set E which is a fixed point of a mapping

is self-similar if and only if the intersections

where
s is the Hausdorff dimension of
E and
Hs denotes
Hausdorff measure. This is clear in the case of the Sierpinski gasket (the intersections are just points), but is also true more generally:
Theorem. Under the same conditions as the previous theorem, the unique fixed point of ψ is self-similar.
[]See also
[]Historical references
[]Notes
[]References




 and
and  , the
, the 
 is the
is the  such that there is some (indexed) collection of
such that there is some (indexed) collection of 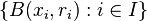 covering
covering 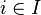 which satisfies
which satisfies  . (One can assume, with no loss of generality, that the index set
. (One can assume, with no loss of generality, that the index set 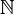 . Here, we use the standard convention that
. Here, we use the standard convention that 
 may be defined as the
may be defined as the 

 holds for some constant
holds for some constant  . A partial converse is provided by
. A partial converse is provided by  is a finite or countable union, then
is a finite or countable union, then

 , the Hausdorff dimension of
, the Hausdorff dimension of  is bounded from above by the Hausdorff dimension of
is bounded from above by the Hausdorff dimension of